Selected ATcT [1, 2] enthalpy of formation based on version 1.122 of the Thermochemical Network [3]
This version of ATcT results was partially described in Ruscic et al. [4],
and was also used for the initial development of high-accuracy ANLn composite electronic structure methods [5].
|
| Species Name |
Formula |
Image |
ΔfH°(0 K) |
ΔfH°(298.15 K) |
Uncertainty |
Units |
Relative
Molecular
Mass |
ATcT ID |
| Nitrous acid | HONO (g) |  | -73.018 | -78.675 | ± 0.079 | kJ/mol | 47.01348 ±
0.00061 | 7782-77-6*0 |
| Representative Geometry of HONO (g) |
| | | spin ON spin OFF | | | Top contributors to the provenance of ΔfH° of HONO (g)The 20 contributors listed below account only for 83.4% of the provenance of ΔfH° of HONO (g).
A total of 42 contributors would be needed to account for 90% of the provenance.
Please note: The list is limited to 20 most important contributors or, if less, a number sufficient to account for 90% of the provenance. The Reference acts as a further link to the relevant references and notes for the measurement. The Measured Quantity is normaly given in the original units; in cases where we have reinterpreted the original measurement, the listed value may differ from that given by the authors. The quoted uncertainty is the a priori uncertainty used as input when constructing the initial Thermochemical Network, and corresponds either to the value proposed by the original authors or to our estimate; if an additional multiplier is given in parentheses immediately after the prior uncertainty, it corresponds to the factor by which the prior uncertainty needed to be multiplied during the ATcT analysis in order to make that particular measurement consistent with the prevailing knowledge contained in the Thermochemical Network.
| Contribution
(%) | TN
ID | Reaction | Measured Quantity | Reference | | 20.9 | 1394.8 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -1.44 ± 0.10 kJ/mol | Vosper 1976, 3rd Law | | 15.0 | 988.2 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 52400 ± 10 cm-1 | Dingle 1975 | | 15.0 | 988.1 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 52400 ± 10 cm-1 | Callear 1970 | | 11.6 | 988.4 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 52408 ± 10 (×1.139) cm-1 | Kley 1973, Miescher 1974, est unc | | 3.3 | 1394.2 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -1.25 ± 0.25 kJ/mol | Wayne 1951, 3rd Law | | 2.7 | 988.3 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 52420 ± 12 (×1.957) cm-1 | Miescher 1974, Huber 1979 | | 2.3 | 1395.3 | ONNO2 (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -3.26 ± 0.15 (×1.915) kJ/mol | Vosper 1976, 3rd Law | | 2.2 | 943.3 | N2 (g) → N+ (g) + N (g) | ΔrH°(0 K) = 24.2880 ± 0.0009 eV | Tang 2005 | | 1.8 | 943.1 | N2 (g) → N+ (g) + N (g) | ΔrH°(0 K) = 24.2888 ± 0.0010 eV | Tang 2005 | | 1.8 | 943.2 | N2 (g) → N+ (g) + N (g) | ΔrH°(0 K) = 24.2883 ± 0.0010 eV | Tang 2005 | | 1.4 | 117.2 | 1/2 O2 (g) + H2 (g) → H2O (cr,l) | ΔrH°(298.15 K) = -285.8261 ± 0.040 kJ/mol | Rossini 1939, Rossini 1931, Rossini 1931b, note H2Oa, Rossini 1930 | | 0.9 | 1204.3 | (NH4)NO3 (cr,l) → N2 (g) + 1/2 O2 (g) + 2 H2O (cr,l) | ΔrH°(293.65 K) = -49.44 ± 0.06 kcal/mol | Becker 1934 | | 0.6 | 991.4 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 626.47 ± 0.56 kJ/mol | Harding 2008 | | 0.5 | 990.10 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 149.82 ± 0.15 kcal/mol | Karton 2007a, Karton 2008 | | 0.5 | 988.6 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 6.503 ± 0.004 (×1.682) eV | Brewer 1956, Frisch 1965 | | 0.4 | 1351.4 | HNO (g) → H (g) + N (g) + O (g) | ΔrH°(0 K) = 823.10 ± 0.56 kJ/mol | Harding 2008 | | 0.4 | 989.10 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 149.78 ± 0.16 kcal/mol | Feller 2014 | | 0.4 | 991.2 | NO (g) → N (g) + O (g) | ΔrH°(0 K) = 626.74 ± 0.70 kJ/mol | Harding 2008 | | 0.4 | 1002.1 | 1/2 N2 (g) + 1/2 O2 (g) → NO (g) | ΔrH°(0 K) = 90.0 ± 0.8 kJ/mol | Szakacs 2011 | | 0.4 | 1394.1 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -1.33 ± 0.69 kJ/mol | Wayne 1951, 3rd Law |
| Top 10 species with enthalpies of formation correlated to the ΔfH° of HONO (g) | Please note: The correlation coefficients are obtained by renormalizing the off-diagonal elements of the covariance matrix by the corresponding variances.
The correlation coefficient is a number from -1 to 1, with 1 representing perfectly correlated species, -1 representing perfectly anti-correlated species, and 0 representing perfectly uncorrelated species.
| Correlation
Coefficent
(%) | Species Name | Formula | Image | ΔfH°(0 K) | ΔfH°(298.15 K) | Uncertainty | Units | Relative
Molecular
Mass | ATcT ID | | 100.0 | Nitrous acid | HONO (g, trans) |  | -73.018 | -79.162 | ± 0.079 | kJ/mol | 47.01348 ±
0.00061 | 7782-77-6*1 | | 82.2 | Nitrogen dioxide | ONO (g) | ![O=[N]=O](../images/44.png) | 36.856 | 34.049 | ± 0.065 | kJ/mol | 46.00554 ±
0.00060 | 10102-44-0*0 | | 82.2 | Nitric oxide | NO (g) | ![[N]=O](../images/39.png) | 90.617 | 91.121 | ± 0.065 | kJ/mol | 30.00614 ±
0.00031 | 10102-43-9*0 | | 82.1 | Nitrosyl ion | [NO]+ (g) | ![N#[O+]](../images/198.png) | 984.485 | 984.479 | ± 0.065 | kJ/mol | 30.00559 ±
0.00031 | 14452-93-8*0 | | 80.0 | Dinitrogen tetraoxide | O2NNO2 (g) | 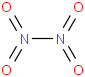 | 20.15 | 10.86 | ± 0.14 | kJ/mol | 92.0111 ±
0.0012 | 10544-72-6*0 | | 79.4 | Nitrosyl chloride | ClNO (g) |  | 54.451 | 52.549 | ± 0.067 | kJ/mol | 65.45884 ±
0.00095 | 2696-92-6*0 | | 77.6 | Dinitrogen dioxide | ONNO (g, cis) | 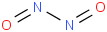 | 172.89 | 171.12 | ± 0.14 | kJ/mol | 60.01228 ±
0.00062 | 16824-89-8*2 | | 77.6 | Dinitrogen dioxide | ONNO (g) | 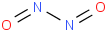 | 172.89 | 171.12 | ± 0.14 | kJ/mol | 60.01228 ±
0.00062 | 16824-89-8*0 | | 75.6 | Nitrogen sesquioxide | ONNO2 (g) | [O]](../images/251.png) | 90.72 | 86.15 | ± 0.15 | kJ/mol | 76.01168 ±
0.00091 | 10544-73-7*0 | | 58.1 | Dinitrogen tetraoxide | O2NNO2 (cr,l) | 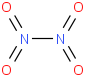 | -37.87 | -27.02 | ± 0.19 | kJ/mol | 92.0111 ±
0.0012 | 10544-72-6*500 |
| Most Influential reactions involving HONO (g)Please note: The list, which is based on a hat (projection) matrix analysis, is limited to no more than 20 largest influences.
| Influence
Coefficient | TN
ID | Reaction | Measured Quantity | Reference | | 1.000 | 1388.1 | HONO (g, trans) → HONO (g) | ΔrH°(0 K) = 0 ± 0 cm-1 | triv, Ruscic G3B3 | | 0.725 | 1394.8 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -1.44 ± 0.10 kJ/mol | Vosper 1976, 3rd Law | | 0.126 | 1395.3 | ONNO2 (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -3.26 ± 0.15 (×1.915) kJ/mol | Vosper 1976, 3rd Law | | 0.116 | 1394.2 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -1.25 ± 0.25 kJ/mol | Wayne 1951, 3rd Law | | 0.015 | 1394.1 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -1.33 ± 0.69 kJ/mol | Wayne 1951, 3rd Law | | 0.015 | 1394.4 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(323 K) = 2.57 ± 0.22 (×3.152) kJ/mol | Ashmore 1961, 3rd Law | | 0.014 | 1394.6 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(296 K) = -0.97 ± 0.39 (×1.834) kJ/mol | Waldorf 1963, 3rd Law | | 0.012 | 1394.3 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrG°(298.15 K) = -1.17 ± 0.75 kJ/mol | Karavaev 1962, Wayne 1951, 3rd Law | | 0.003 | 1394.9 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrH°(298.15 K) = -39.3 ± 0.9 (×1.542) kJ/mol | Vosper 1976, 2nd Law | | 0.002 | 1395.1 | ONNO2 (g) + H2O (g) → 2 HONO (g) | ΔrH°(0 K) = 1.05 ± 0.30 (×1.795) kcal/mol | Varma 1976 | | 0.001 | 1394.7 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrH°(298.15 K) = -9.55 ± 0.5 kcal/mol | Waldorf 1963, 2nd Law, est unc | | 0.000 | 1395.2 | ONNO2 (g) + H2O (g) → 2 HONO (g) | ΔrH°(298.15 K) = 1.9 ± 1.2 (×3.018) kJ/mol | Vosper 1976, 2nd Law | | 0.000 | 1394.5 | NO (g) + ONO (g) + H2O (g) → 2 HONO (g) | ΔrH°(323 K) = -37.77 ± 0.65 (×4.757) kJ/mol | Ashmore 1961, 2nd Law |
|
|
|
References
|
|
1
|
|
B. Ruscic, R. E. Pinzon, M. L. Morton, G. von Laszewski, S. Bittner, S. G. Nijsure, K. A. Amin, M. Minkoff, and A. F. Wagner,
Introduction to Active Thermochemical Tables: Several "Key" Enthalpies of Formation Revisited.
J. Phys. Chem. A 108, 9979-9997 (2004)
[DOI: 10.1021/jp047912y]
|
|
2
|
|
B. Ruscic, R. E. Pinzon, G. von Laszewski, D. Kodeboyina, A. Burcat, D. Leahy, D. Montoya, and A. F. Wagner,
Active Thermochemical Tables: Thermochemistry for the 21st Century.
J. Phys. Conf. Ser. 16, 561-570 (2005)
[DOI: 10.1088/1742-6596/16/1/078]
|
|
3
|
|
B. Ruscic and D. H. Bross,
Active Thermochemical Tables (ATcT) values based on ver. 1.122 of the Thermochemical Network (2016); available at ATcT.anl.gov |
|
4
|
|
B. Ruscic,
Active Thermochemical Tables: Sequential Bond Dissociation Enthalpies of Methane, Ethane, and Methanol and the Related Thermochemistry.
J. Phys. Chem. A 119, 7810-7837 (2015)
[DOI: 10.1021/acs.jpca.5b01346]
|
|
5
|
|
S. J. Klippenstein, L. B. Harding, and B. Ruscic,
Ab initio Computations and Active Thermochemical Tables Hand in Hand: Heats of Formation of Core Combustion Species.
J. Phys. Chem. A 121, 6580-6602 (2017)
[DOI: 10.1021/acs.jpca.7b05945]
|
|
6
|
|
B. Ruscic,
Uncertainty Quantification in Thermochemistry, Benchmarking Electronic Structure Computations, and Active Thermochemical Tables.
Int. J. Quantum Chem. 114, 1097-1101 (2014)
[DOI: 10.1002/qua.24605]
|
|
|
|
Formula
|
|
The aggregate state is given in parentheses following the formula, such as: g - gas-phase, cr - crystal, l - liquid, etc.
|
|
|
Uncertainties
|
The listed uncertainties correspond to estimated 95% confidence limits, as customary in thermochemistry (see, for example, Ruscic [6]).
Note that an uncertainty of ± 0.000 kJ/mol indicates that the estimated uncertainty is < ± 0.0005 kJ/mol.
|
|
|
Website Functionality Credits
|
The reorganization of the website was developed and implemented by David H. Bross (ANL).
The find function is based on the complete Species Dictionary entries for the appropriate version of the ATcT TN.
The molecule images are rendered by Indigo-depict.
The XYZ renderings are based on Jmol: an open-source Java viewer for chemical structures in 3D. http://www.jmol.org/.
|
|
|
Acknowledgement
|
|
This work was supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences under Contract No. DE-AC02-06CH11357.
|
|
Page generated: 04/05/2025
|







